Stress and Strain Overview
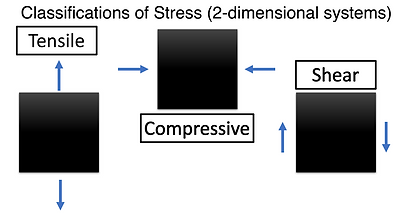
Stress is defined as "the measure of the intensity of an internal load acting on a cross-section on an object". Stress usually exists as either shear or normal stress. Normal stress can be further classified as either tensile or compressive.Stress is referred to as tensile if "pull" is occurring. Pulling of a sample causes it to extend length-wise therefore "elongating" it. Stress that shortens a material lengthwise through "push" motion is defined as compressive. Shear stress is a phenomenon that occurs when forces act parallel to an exposed surface. This is most common when a material is being cut. For example, shears used to cut sheep wool can be seen as a shear force.
Strain is defined as "a measure of the deformation of an object with respect to its initial length, or a measure of the intensity of change in the shape of a body". For this reason, the strain is denoted by the change in length and in some cases a percentage.
The equations for strain can be expressed as either normal/engineering or true strain.


True Stress and True Strain vs Engineering Stress and Strain
Engineering stress and strain are used as a rough approximation. This is because they are often used to predict certain values or to predict the limits of a material. In a diagram of engineering stress-strain, the line will drop after a certain point. This represents the material failing. These values can be predicted through the use of a tensile test or the condition and effects a material will receive while put under certain conditions.
True stress-strain represents the actual values of the relationship between stress and strain.
The elastic region of material will always be linear and the same in engineering stress and the true stress.
The difference is apparent in the plastic region of the graphs after necking occurs. This is because true stress-strain accounts for the change in the area caused by deformation.
Stress-Strain Plot Overview
The relationship between stress and strain can be represented in a diagram known as the stress-strain plot. Stress is plotted vertically (dependent) and strain is plotted horizontally (independent). The value of stress is determined by the value of the strain being exhibited on the material. The strain occurring at an object at a constant rate is referred to as "Constant Strain Rate".
The stress-strain plot can be derived from tensile strength tests
-
Tensile tests are used to determine how much force or load a material can withstand until it breaks or fails
-
They are done by extending a material length-wise along its axis
-
-
They can also be used to determine the relationship between stress and strain
Regions in the Stress-Strain Plot
The low strain regions of the plot are usually linear (Elastic Region)
-
This means there is a direct and constant relationship between stress and strain
-
Deformation occurring in this portion can be reversed by removing the force
-
Similar to how rubber bands deform when tensile stress or pulling occurs, but when the force is removed the rubber band returns to normal
-
-
The linear relationship between stress and strain can be represented in Hooke's Law
-
Also known as the law of elasticity
-
It states that the force (F) needed to extend or compress a spring by some distance (x) scales linearly with respect to that distance
-
-
The relationship/ratio between stress and strains shown in the equation is Young's Modulus
-
-
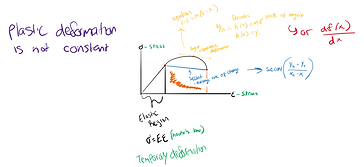
The point in which the relationship is no longer linear is known as the plastic region
-
This means that the change occurring is not simply reversible
-
Permanent plastic deformation
-
Caused by atom bonds breaking at dislocations
-
Deformation is permanent and remains after the load is removed
-
Necking is the point that represents the rapid reduction of the material relative to deformation
-
In a stress-strain graph representing engineering stress-strain, the necking point is the ultimate tensile strength or the point prior to material failure
Stress-Strain Curve Equations (Elastic Region)
The elastic region will always be linear because any deformation caused by the applied load can be instantly reversed if the applied force is taken away. This rule is known as Hooke Law which states " that the force (F) needed to extend or compress a spring by some distance (x) scales linearly with respect to that distance". In mathematical terms, it translates to "stress is equal to the value of young modulus multiplied by strain".
As you've most likely learned in algebra the Stress-Strain equations for the linear region are modeled after the slope-intercept equation for denoting the linear relationship between a dependent and independent variable. The "y" or dependent variable, in this case, represents the value of stress. The "M" variable represents the slope of the stress/strain curve or the value of the young's modulus. The "X" or the independent variable represents the value of strain.
Relationship between Ductile and Brittle
Ductile Materials
-
Can undergo large quantities of plastic deformation before failure
Brittle Materials
-
Will typically fail or break before plastic deformation can occur
-
Solid glass and ceramics are examples of brittle materials
Temperature can be a major factor in ductility and brittleness. For example, steel can be very ductile when heated up or very brittle when cooled down. This explains why a blacksmith can reshape metal when it is hot causing it to bend but once it cools it will shatter when exposed to a significant amount of stress.

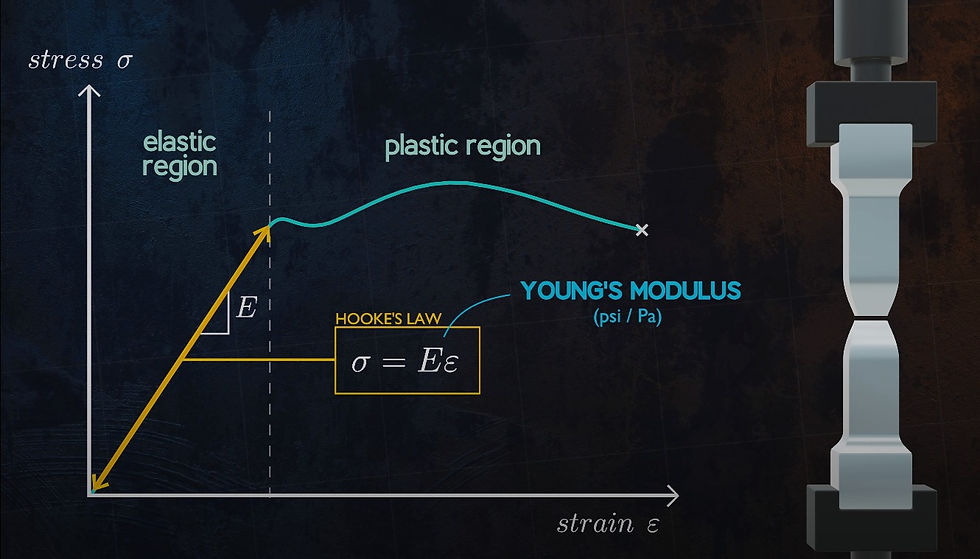
Represents how Hooke's law factors into the elastic region of the stress-strain plot
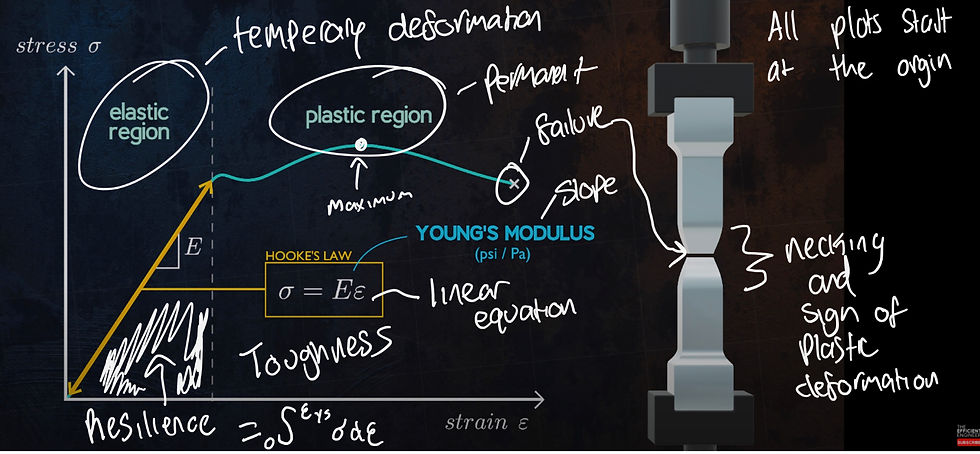
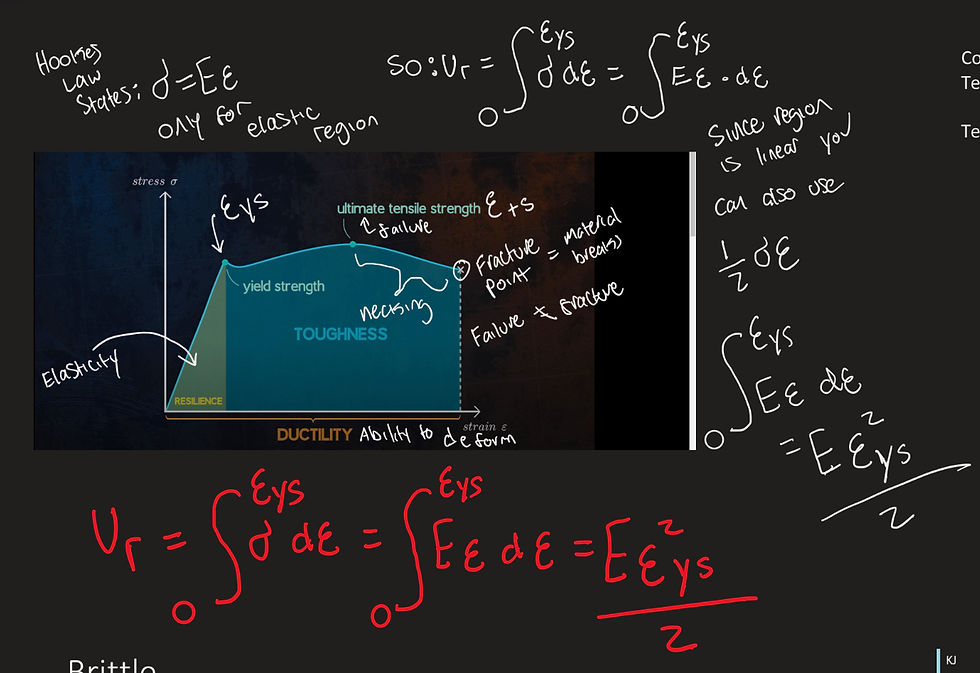

Represents how Hooke's law factors into the elastic region of the stress-strain plot
Mathematics Connection:
Graphics were taken from "The Efficient Engineer"
Strength
Strength is the measure of the stress a material can withstand until it fails or permanently deforms
Strength is measured in Pascals and Psi
Ultimate Strength:
-
The maximum stress a material can withstand during a test
Yield Strength:
-
The point in which the amount of stress applied causes the material to deform plastically
-
This means it has been permanently deformed
-
-
Tensile yield strengths are shown for ductile materials
Toughness/ Ductility
Material toughness is a measure of the ability of a material to absorb energy to fracture. It can also be rephrased to the amount of plastic deformation that is required to occur before failure. It can be identified as the area under the stress-strain curve. Despite the graphic, it refers to the entire area including the portion in the elastic region.
The toughness of a material is an extremely important characteristic to consider when using the material in instances in which they will be tasked with undergoing large quantities of stress and load. These materials will be able to absorb lots of load before failure.
Hardness
Essentially, the hardness of a material is a measure of its resistance surface or superficial deformation/damage. This refers to a material's ability to not get scratched or scraped. For this reason, diamond is considered one of the hardest materials on the planet. Diamond cannot be scratched or chipped unless exposed to an obscene amount of force.
